二分查找

三分查找比二分查找快，但二分查找使用得更广泛的原因在于，在最坏情况下，三分查找比较次数要比二分查找要多。（比如1-9，最坏情况就是1和9）

[TOC]

一、复杂度皆为O(logn)

二分查找的基本思想是将n个元素分成大致相等的两部分，去a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.

时间复杂度无非就是while循环的次数！

总共有n个元素，

渐渐跟下去就是n,n/2,n/4,....n/2^k，其中k就是循环的次数

由于你n/2^k取整后>=1

即令n/2^k=1

可得k=log2n,（是以2为底，n的对数）

递归的次数和深度都是log2 n,每次所需要的辅助空间都是常数级别的： 时间复杂度 : O(log2 n) 空间复杂度：O(log2 n)

二、适用场景：有序

如果在乱序的情况下使用，暴力算法反而会更快一些。

var num = 1000000;
var randomNum = Math.ceil(Math.random()*num);
document.title = randomNum;
var arr = [];
for(var i=1;i<=num;i++){
	arr.push(i);
}
arr.sort(function(){
	return Math.random() - 0.5;
});

// 暴力查找
function show1(arr,randomNum){
	console.time(1);
	for(var i=0;i<arr.length;i++){
		if( arr[i] == randomNum ){
			console.timeEnd(1);
			return arr[i];
		}
	}
}

// 二分查找
function show2(arr,randomNum){
	console.time(2);
	arr.sort(function(n1,n2){
		return n1 - n2;
	});
	var first = 0;
	var last = arr.length-1;
	while( first <= last ){
		var mIndex = Math.floor((first + last)/2);
		if( randomNum < arr[mIndex] ){
			last = mIndex - 1;
		}
		else if( randomNum > arr[mIndex] ){
			first = mIndex + 1;
		}
		else{
			console.timeEnd(2);
			return arr[mIndex];
		}
	}
}

console.log(show1(arr,randomNum));
console.log(show2(arr,randomNum));

// 1: 1.42822265625ms
// 274610
// 2: 499.859130859375ms
// 274610

有序的情况下则是

// 1: 2.9248046875ms
// 256953
// 2: 0.017822265625ms
// 256953

三、具体实现

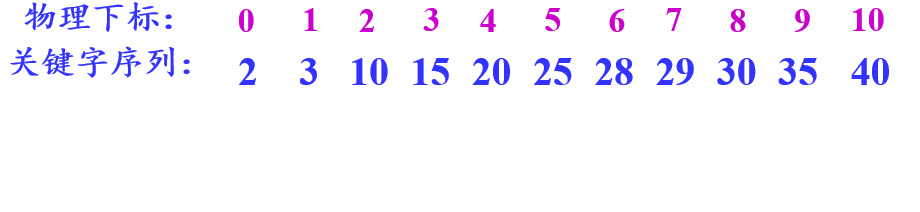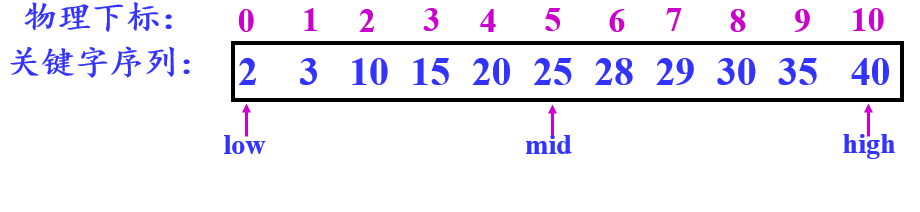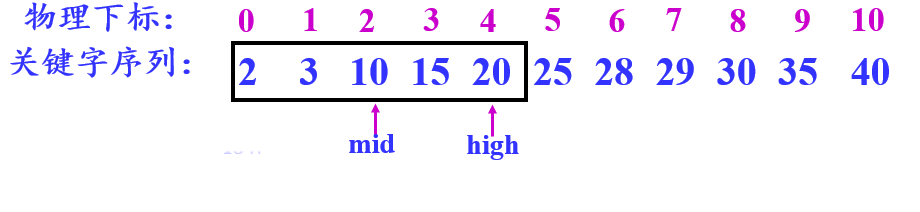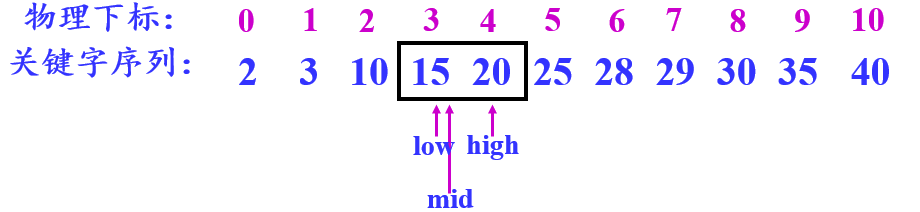
function binarySearch(target, arr) {
    let low = 0;
    let high = arr.length - 1;
    while (low <= high) {
        let mid = Math.floor((low + high) / 2);
        if (target == arr[mid]) {
            return arr[mid];
        } else if (target < arr[mid]) {
            high = mid - 1;
        } else {
            low = mid + 1;
        }
    }
    return false;
}