十大经典排序算法

参考资料：https://www.cnblogs.com/onepixel/p/7674659.html (opens new window)

[TOC]

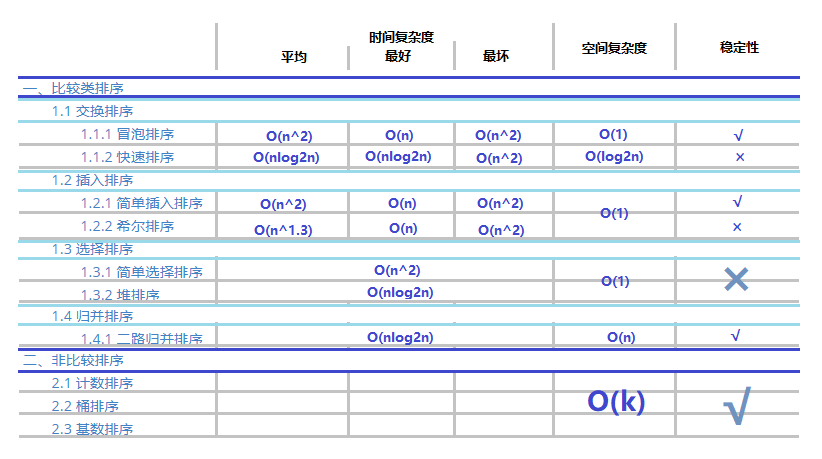
一、比较类排序

1.1 交换排序

1.1.1 冒泡排序

按顺序一个个的排，大的就往后冒泡。

function bubbleSort(arr) {
    let len = arr.length;
    // 要对n-1个数进行一轮两两交换
    for (let i = 0; i < len - 1; i++) {
        // 最后面排好序的数无需再进行两两交换
        for (let j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                arr[j] += arr[j + 1];
                arr[j + 1] = arr[j] - arr[j + 1];
                arr[j] -= arr[j + 1];
            }
        }
    }
    return arr;
}

// 时间复杂度
// 平均：O(n^2)
// 最坏：O(n^2)
// 最好：O(n)
// 空间复杂度
// O(1)
// 稳定

1.1.2 快速排序

// 一趟划分
// 时间复杂度O(n)
function partition(arr, low, high) {
    // 基准
    let mid = arr[low];
    // 从两端交替向中间扫描，直至i=j为止
    while (low < high) {
        // 从右向左扫描，直至找到比基准小的值
        while (high > low && arr[high] >= mid) {
            high--;
        }
        arr[low] = arr[high];
        // 从左向右扫描，直至找到比基准大的值
        while (low < high && arr[low] <= mid) {
            low++;
        }
        arr[high] = arr[low];
    }
    // 此时arr[low]的值即为基准
    arr[low] = mid;
    return low;
}

// 时间复杂度O(log2n)
function quickSort(arr, low = 0, high = arr.length - 1) {
    // 区间内至少存在两个元素的情况
    if (low < high) {
        let i = partition(arr, low, high);
        quickSort(arr, low, i - 1);
        quickSort(arr, i + 1, high);
    }
    return arr;
}

// 时间复杂度
// 平均：O(nlog2n)
// 最坏：O(n^2)
// 最好：O(nlog2n)
// 空间复杂度
// O(1og2n)
// 不稳定	[5,2,4,8,7,4]->[4,2,8,7,4]

1.2 插入排序

1.2.1 简单插入排序

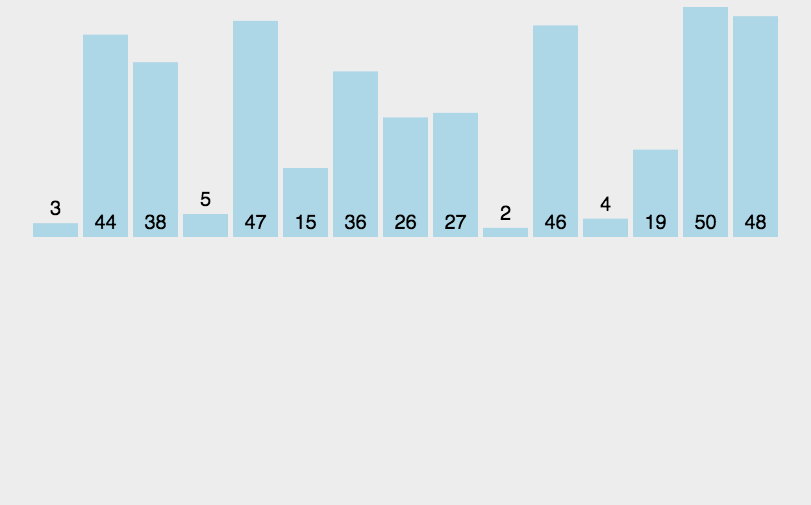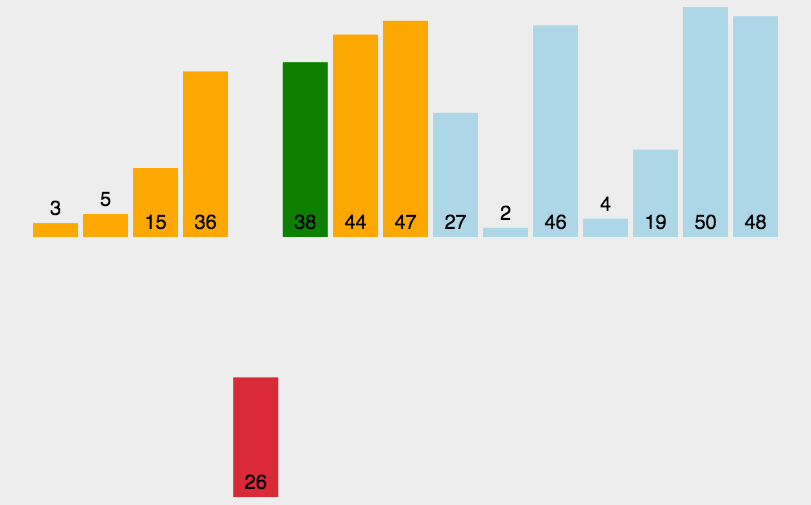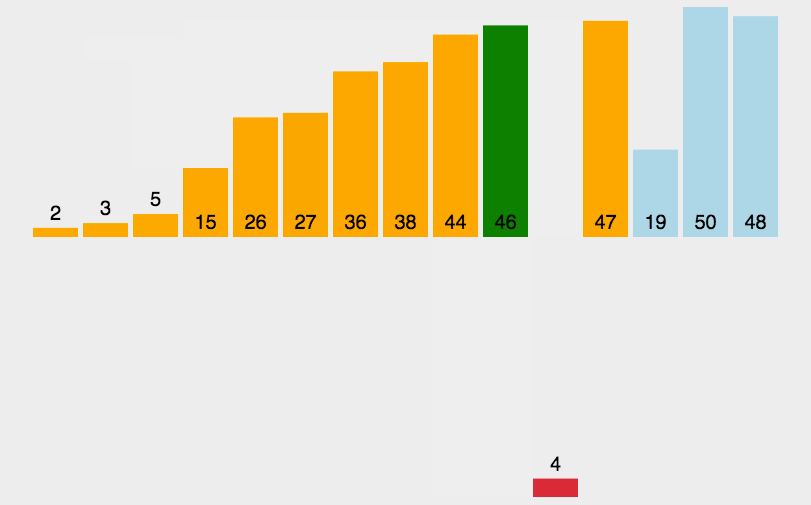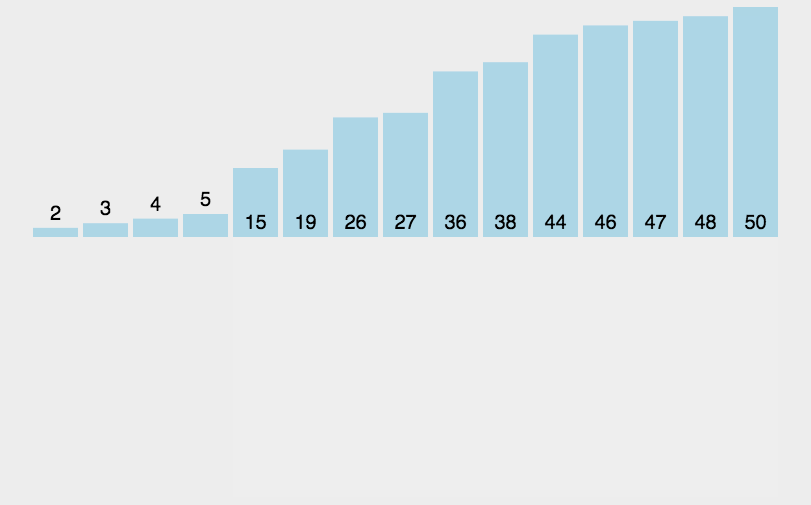
function insertSort(arr) {
    let len = arr.length;
    for (let i = 1; i < len; i++) {
        if (arr[i] < arr[i - 1]) {
            // 出现反序时，确定要插入的位置
            // 存储要插入的值，避免被后移值覆盖
            let tmp = arr[i];
            let j = i - 1;
            // 找插入的位置
            do {
                arr[j + 1] = arr[j];
                j--;
            } while (j >= 0 && arr[j] > tmp);
            arr[j+1]=tmp;
        }
    }
    return arr;
}

// 时间复杂度
// 平均：O(n^2)
// 最坏：O(n^2)
// 最好：O(n)
// 空间复杂度
// O(1)
// 稳定

1.2.2 希尔排序

// 减小增量+直接插入排序
function shellSort(arr) {
    let len = arr.length;
    // 增量置初值
    let gap = Math.floor(len / 2);
    while (gap) {
        for (let i = gap; i < len; i++) {
            // 插入排序
            let tmp = arr[i];
            let j = i - gap;
            while (j >= 0 && tmp < arr[j]) {
                arr[j + gap] = arr[j];
                j = j - gap;
            }
            arr[j + gap] = tmp;

        }
        gap = Math.floor(gap / 2);
    }
    return arr;
}

// 时间复杂度
// 平均：O(n^1.3)
// 最坏：O(n^2)
// 最好：O(n)
// 空间复杂度
// O(1)
// 不稳定

1.3 选择排序

1.3.1 简单选择排序

在未排列区找到最小的数，并放置于已排列区的末端。

function selectSort(arr) {
    let len = arr.length;
    for (let i = 0; i < len - 1; i++) {

        let minIndex = i;
        for (let j = i+1; j < len; j++) {
          if (arr[minIndex] > arr[j]) {
            minIndex = j;
          }
        }

        let temp = arr[i]
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
}

// 时间复杂度
// 平均：O(n^2)
// 最坏：O(n^2)
// 最好：O(n^2)
// 空间复杂度
// O(1)
// 不稳定	[5,6,1] -> [1,6,5]

1.3.2 堆排序

// 将关键字看成一棵完全二叉树的顺序存储结构
// 根节点为arr[i]，则左孩子为arr[2i],右孩子为arr[2i+1]

// 筛选算法：以arr[low]为根结点的左子树和右子树均为大根堆(根大于左右)
function sift(arr, low, high) {
    // arr[j]是arr[i]的左孩子
    let i = low,
        j = 2 * i;
    let tmp = arr[i];
    while (j <= high) {
        // 若右孩子比较大，把j指向右孩子
        if (j < high && arr[j] < arr[j + 1]) {
            j++;
        }
        // 若根结点小于最大孩子的关键字
        if (tmp < arr[j]) {
            // 将arr[j]调整到双亲结点位置上
            arr[i] = arr[j];
            // 修改i和j值，以便继续向下筛选
            i = j;
            j = 2 * i;
        } else {
            // 若根结点大于等于最大孩子关键字，筛选结束
            break;
        }
    }
    // 被筛选结点放入最终位置
    arr[i] = tmp;
}

function heapSort(arr) {
    let len = arr.length;
    // 循环建立初始堆，调用sift算法
    // 即从最后一个分支结点开始筛选
    // 大者上浮，小者被筛选下去
    for (let i = Math.floor(len / 2); i >= 0; i--) {
        sift(arr, i, len-1);
    }
    // 进行n-1趟完成队排序，每一趟堆中元素个数减1
    for (let i = len - 1; i >= 1; i--) {
        // 将最后一个元素与根arr[0]交换
        arr[0] ^= arr[i];
        arr[i] ^= arr[0];
        arr[0] ^= arr[i];
        sift(arr, 0, i - 1);
    }
    return arr;
}

// 时间复杂度
// 平均：O(nlog2n)
// 最坏：O(nlog2n)
// 最好：O(nlog2n)
// 空间复杂度
// O(1)
// 不稳定

1.4 归并排序

参考资料：https://www.cnblogs.com/chengxiao/p/6194356.html (opens new window)

1.4.1 二路归并排序

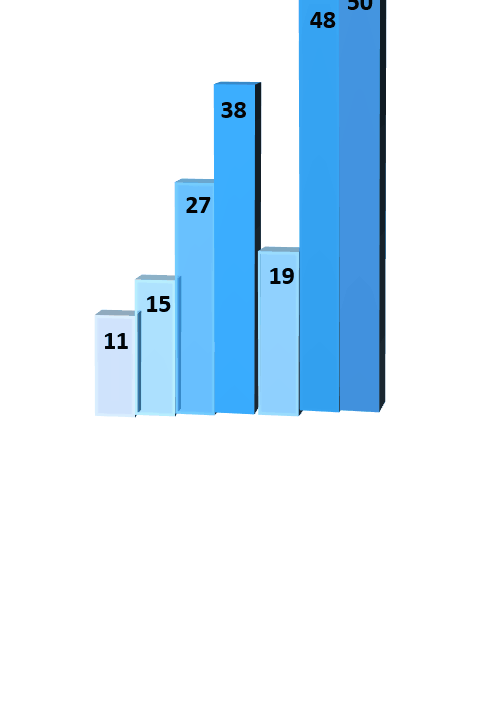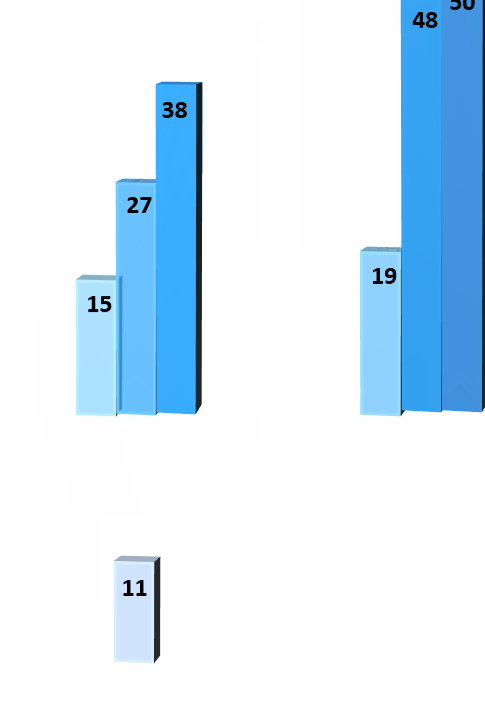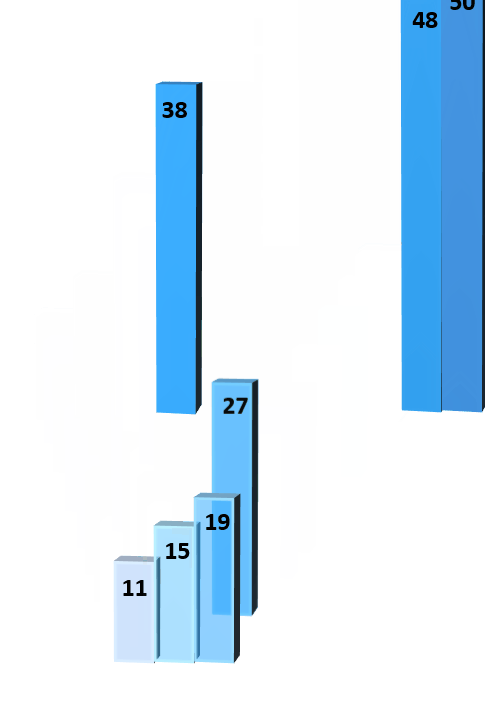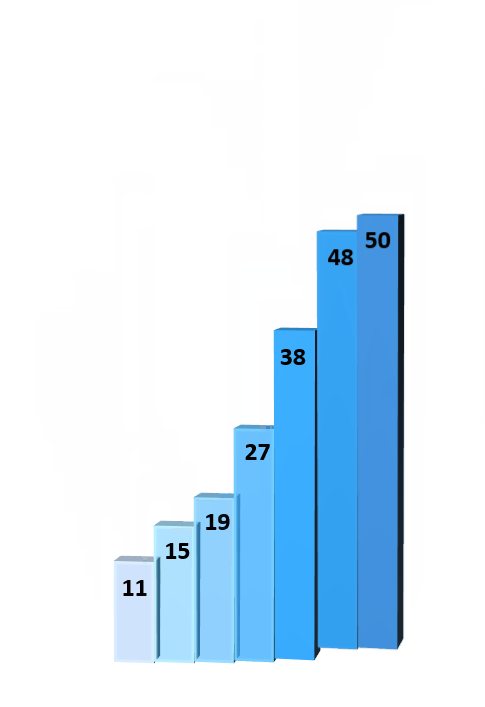
// 分治法
function mergeSort(arr) {
    let len = arr.length;
    if (len < 2) {
        return arr;
    }

    // 分阶段
    // 递归次数-时间复杂度：完全二叉树深度-O(log2n)
    let mid = Math.floor(len / 2);
    let left = arr.slice(0, mid);
    let right = arr.slice(mid);
    return merge(mergeSort(left), mergeSort(right));
}

// 治阶段
// 时间复杂度O(n)
function merge(left, right) {
    let result = [];
    while (left.length && right.length) {
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift())
        }
    }

    // while (left.length) {
    //   // 若使用concat()会创建新的数组
    //   result.push(left.shift());

    // }
    // while (right.length) {
    //   result.push(right.shift());

    // }

    // ES6写法
    if (left.length) {
        result.push(...left);
    }
    if (right.length) {
        result.push(...right);
    }
    return result;
}

// 时间复杂度
// 平均：O(nlog2n)
// 最坏：O(nlog2n)
// 最好：O(nlog2n)
// 空间复杂度
// 每次二路归并都需要一个辅助数组来暂存两个有序子表归并的结果，而每次归并后都会释放空间。
// 但最后一趟需要所有元素参与归并，所以总的辅助空间复杂度为O(n)。
// 稳定

示例：[56,3,63,23,57,8,4,7,9,41]（想想二叉树）
分-56 3 63 23 57
分-56 3
分-56
分-3
并-3 56
分-63 23 57
分-63
分-23 57
分-23
分-23 57
并-23 57 63
并-3 23 56 57 63
分-8 4 7 9 41
……

二、非比较排序

2.1 计数排序

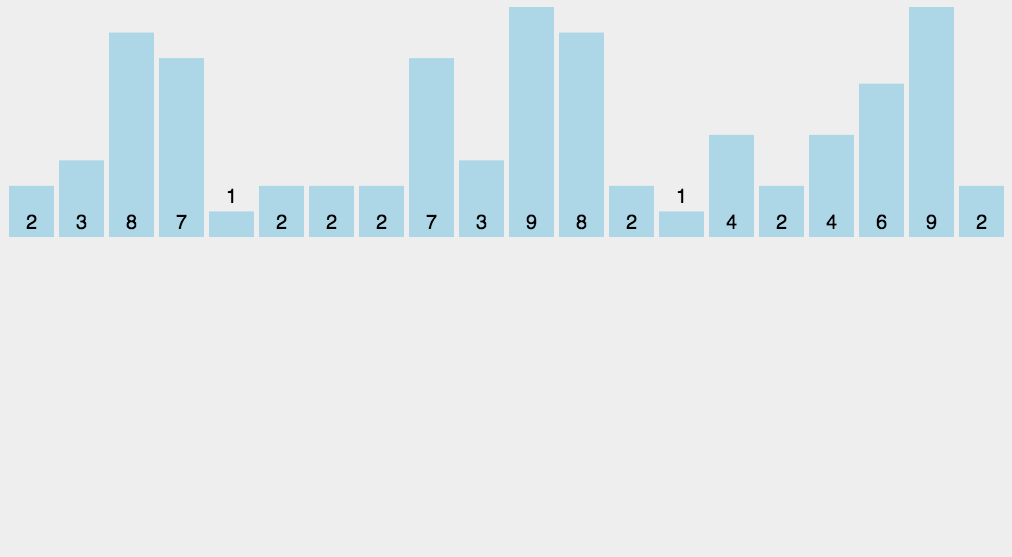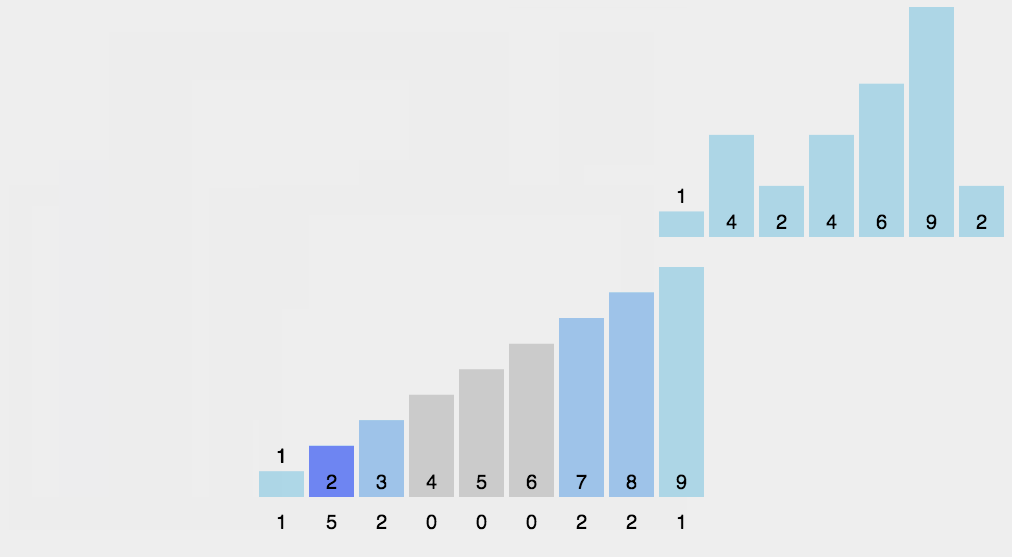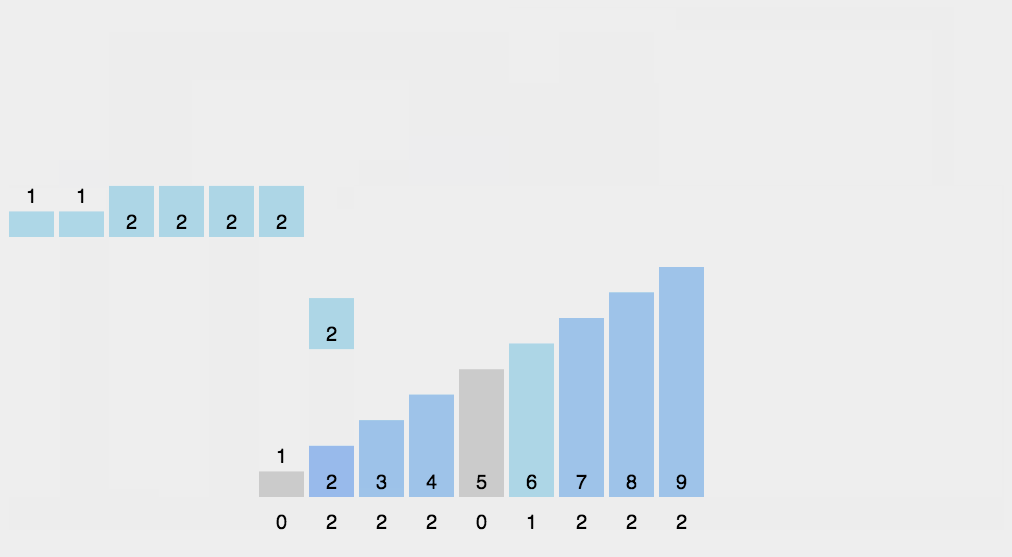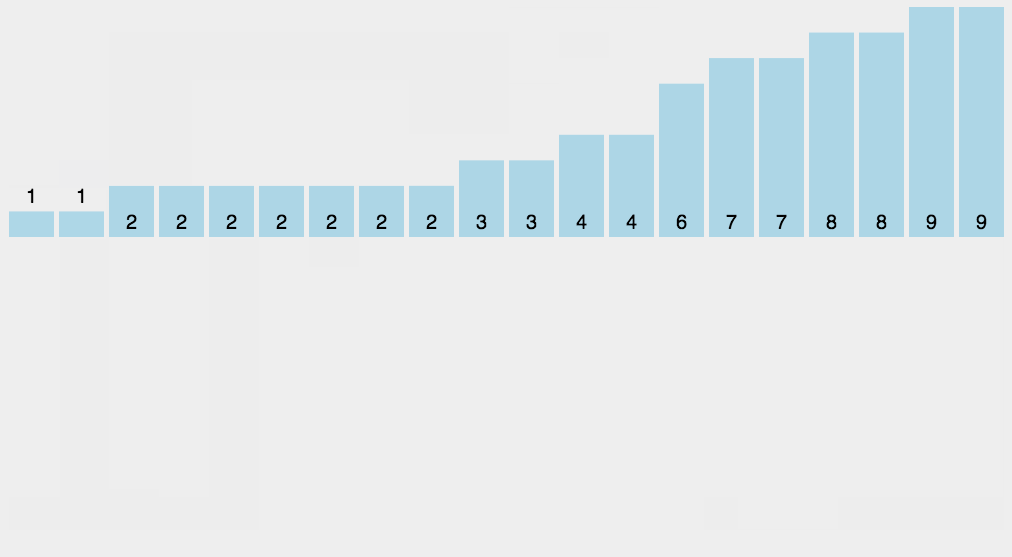
function countSort(arr) {
    let len = arr.length;
    // 找出待排序的数组中最大和最小的数字
    let min = arr[0],
        max = arr[0];
    for (let i = 1; i < len; i++) {
        if (arr[i] < min) min = arr[i];
        else if (arr[i] > max) max = arr[i];
    }
    // 初始化计数数组
    let cLen = max - min + 1;
    let countArr = new Array(cLen).fill(0);

    // 计数
    for (let i = 0; i < len; i++) {
        countArr[arr[i]]++;
    }

    // 反向填充目标数组（直接覆盖）
    let j = 0;
    for (let i = 0; i < cLen; i++) {
        while (countArr[i]) {
            arr[j++] = i;
            countArr[i]--;
        }
    }
    return arr;
}

// 输入的元素是 n 个 0 到 k 之间的整数时
// 时间复杂度
// 平均：O(n+k)
// 最坏：O(n+k)
// 最好：O(n+k)
// 空间复杂度
// O(k)
// 稳定

2.2 桶排序

将数字放在对应的桶里，再对每个桶里的数进行排序。

function bucketSort(arr,bucketSize=2){
    let len = arr.length;
    if(len<=1) return arr;

    let min=arr[0],max=arr[0];
    for(let i=1;i<len;i++){
        if(arr[i]<min) min = arr[i];
        else if(arr[i]>max) max=arr[i];
    }

    // 初始化桶
    let bucketCount = Math.ceil((max-min+1)/bucketSize);
    let buckets = new Array(bucketCount);
    for(let i = 0;i<bucketCount;i++){
        buckets[i]=[]
    }

    // 遍历原始数组，将每个元素放入桶中
    for(let i=0;i<len;i++){
        buckets[Math.floor((arr[i]-min)/bucketSize)].push(arr[i]);
    }

    // 对每个桶进行内排序,并输出
    arr = [];
    for(let i = 0;i<bucketCount;i++){
        insertSort(buckets[i]);
        if(buckets[i].length){
            arr.push(...buckets[i]);
        }
    }

    return arr;
}

// 假设有m个桶，每个桶的元素n/m
// 时间复杂度
// 平均：O(n)+m*O(内)
// 空间复杂度
// O(m)
// 稳定

2.3 基数排序

// LSD: least significant digit first(最低位优先)
// radix为基数，digit为关键字位数
// 如果出现负数的情况，只要全部加上负数绝对值最大的值，变为正数即可。
function redixSort(arr, radix, digit) {
    let len = arr.length;

    // 定义二维数组
    let container = new Array(radix);
    for (let i = 0; i < radix; i++) {
        container[i] = [];
    }

    // 从低位到高位循环
    for (let i = 1; i <= digit; i++) {
        // 将待排序的元素放在对应的容器里
        for (let j = 0; j < len; j++) {
            // 次方：不是按位异或^，而是Math.pow(x,y)
            container[Math.floor(arr[j] % Math.pow(10,i)  / Math.pow(10,i-1))].push(arr[j]);
        }

        // 将排序后的元素覆盖未排序（上一次排序）的arr
        arr = [];
        for (let z = 0; z < radix; z++) {
            while(container[z].length){
                arr.push(container[z].shift());
            }
        }

    }
    return arr;
}

// 时间复杂度
// 平均：Od(n+r)
// 最坏：Od(n+r)
// 最好：Od(n+r)
// 空间复杂度
// O(r)
// 稳定

三、排序方法的选择

参考资料：https://blog.csdn.net/FISHBALL1/article/details/52425521 (opens new window)

1. 若n较小（如n≤50），可采用直接插入法或简单选择排序。一般地，直接插入法较好，但简单选择排序移动的元素少于直接插入排序。
2. 若文件初始状态基本有序（指正序），则选用直接插入或冒泡排序为宜。
3. 若n较大,应采用时间复杂度为O(nlog2n)的排序方法，例如快速排序、堆排序或二路归并排序。快速排序是目前基于比较的内排序中被认为较好的方法，当待排序的关键字是随机分布时，快速排序的平均时间最少，但当基本有序时，快速排序的时间复杂度将会变成O(n^2)；但堆排序所需的辅助空间少于快速排序，并且不会出现快速排序可能出现的最坏情况。这两种排序都是不稳定的，若要求排序稳定，则可选用二路归并排序。
4. 若需要将两个有序表合并成一个新的有序表，最好用二路归并排序方法。
5. 基数排序可能在O(n)时间内完成对n个元素的排序。但基数排序只适用于像字符串和整数这类有明显结构特征的关键字，而当关键字的取值范围属于某个无穷集合（例如实数型关键字）时无法使用基数排序。若n很大，元素的关键字位数较少且可以分解时采用基数排序较好。

堆排序相比快速排序的劣处

堆排序下，数据读取的开销变大。

在计算机进行运算的时候，数据不一定会从内存读取出来，而是从一种叫cache的存储单位读取。原因是cache相比内存，读取速度非常快，所以cache会把一部分我们经常读取的数据暂时储存起来，以便下一次读取的时候，可以不必跑到内存去读，而是直接在cache里面找。

• 一般认为读取数据遵从两个原则：

  • temporal locality，也就是不久前读取过的一个数据，在之后很可能还会被读取一遍。

  • 另一个叫spatial locality，也就是说读取一个数据，在它周围内存地址存储的数据也很有可能被读取到。

因此，在读取一个单位的数据(比如1个word)之后，不光单个word会被存入cache，与之内存地址相邻的几个word，都会以一个block为单位存入cache中。另外，cache相比内存小得多，当cache满了之后，会将旧的数据剔除，将新的数据覆盖上去。

​ 在进行堆排序的过程中，由于我们要比较一个数组前一半和后一半的数字的大小，而当数组比较长的时候，这前一半和后一半的数据相隔比较远，这就导致了经常在cache里面找不到要读取的数据，需要从内存中读出来，而当cache满了之后，以前读取的数据又要被剔除。

​ 简而言之快排和堆排读取arr[i]这个元素的平均时间是不一样的。