位运算

# 位运算

[TOC]

底层的计算机语言
平常的数值运算，其本质都是先转换成二进制再进行运算的，而位运算是直接进行二进制运算，所以原则上位运算的执行效率是比较高的。

# 一、符号介绍

运算符	用法	描述
按位与（ AND） (opens new window)	`a & b`	两个位都是1，结果才为1。
按位或（OR） (opens new window)	`a \| b`	两个位都是0，结果才为0.
按位异或（XOR） (opens new window)	`a ^ b`	两个位相同时为0，相异为1。
按位非（NOT） (opens new window)	`~ a`	反转操作数的比特位，即0变成1，1变成0。
左移（L (opens new window)eft shift） (opens new window)	`a << b`	将 `a` 的二进制形式向左移 `b` (< 32) 比特位，右边用0填充。
有符号右移 (opens new window)	`a >> b`	将 a 的二进制表示向右移`b`(< 32) 位，丢弃被移出的位。正数高位补0，低位补1。
无符号右移 (opens new window)	`a >>> b`	将 a 的二进制表示向右移`b`(< 32) 位，丢弃被移出的位，并使用 0 在左侧填充。

# 二、基本应用

n & 1 相当于 n % 2。
- 二进制中偶数的最后一位是0，奇数的最后一位是1，而十进制1在8位二进制中表示为0000 0001。
```
function isOld(n) {
    return n % 2 !== 0;
}

function isOld(n) {
    return n & 1 !== 0;
}
```
1
2
3
4
5
6
7
使用~, >>, <<, >>>, |来取整
- 从概念上讲，按位逻辑操作符按遵守下面规则：
  - 操作数被转换成32位整数，用比特序列（0和1组成）表示。超过32位的数字会被丢弃。
  - 具有32位以上的整数将转换为32位整数，所以小数部分会被舍弃。

// 相当于正数的Math.floor(),负数的Math.ceil()
console.log(~~ 6.83)    // 6
console.log(~~ -6.83)	// -6
console.log(6.83 >> 0)  // 6
console.log(6.83 << 0)  // 6
console.log(6.83 | 0)   // 6

1
2
3
4
5
6

// >>>不可对负数取整
console.log(6.83 >>> 0)   // 6

1
2

a<<b 相当于 a*(2^b)
a>>b 相当于 a/(2^b)

a^a=0;a^0=a;(a^b)^c=a^(b^c) => 交换两位数

a ^= b;	//a = a ^ b 
b ^= a;	//b = a ^ b = (a ^ b) ^ b = a ^ (b ^ b) = a ^ 0 = a 
a ^= b;	//a = a ^ b = (a ^ b) ^ b = (a ^ a) ^ b = b ^ 0 = b

1
2
3

对2^n的数值进行取余运算：a&15 = a%16
求相反数：-a=~a+1=~(a-1) =>~x=-x-1
求绝对值：a>>31==0？a:(~a+1)
取int型变量a的第k位 (k=0,1,2……sizeof(int))，即a>>k&1
整数的平均值：对于两个整数x,y，如果用 (x+y)/2 求平均值，会产生溢出，因为 x+y 可能会大于INT_MAX，但是我们知道它们的平均值是肯定不会溢出的。(x&y)+((x^y)>>1
对于一个整数 x >= 0，判断他是不是2的幂： ((x&(x-1))==0)&&(x!=0)
当一个数满足(num & (num - 1)) === 0，则这个数是2的整数次幂。
- 2的整数次幂的二进制特点：第一位是1，后面都是0。
- 1000...0 - 1 = 0111...1
- 1000...0 & 0111...1 = 0
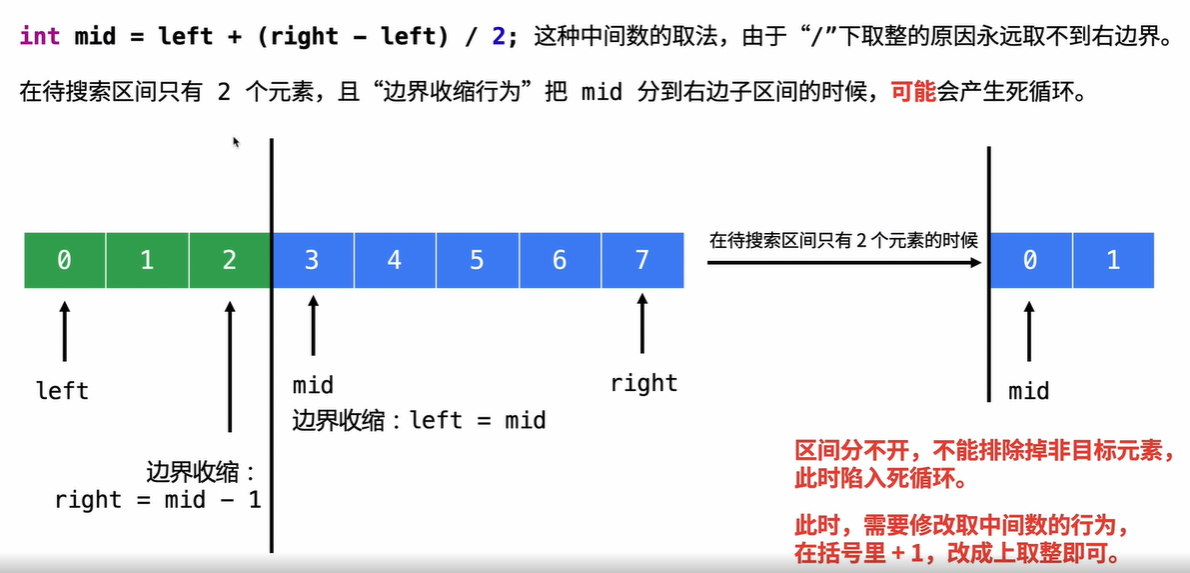
取中位数时，避免计算上出现整型溢出。
- mid = (low + high)/2 或 low + (high - low)/2 都有可能溢出，其中 low + (high - low)/2 会取不到high值。
- mid = (low+high)>>>1，当整型溢出时，会得到负数，再通过无符号右移运算符就可以得到正数。

异步处理 BOM：Browser Object Model 浏览器对象模型

LinHuijuan's Blog

Choose mode

位运算

# 位运算

# 一、符号介绍

# 二、基本应用